How to Calculate Z-Scores in Excel: Tips and Tutorial

Are you struggling to calculate and interpret z-scores in Excel? This comprehensive guide will walk you through the entire process, from basic concepts to advanced techniques. By the end, you’ll be confidently using z-scores for statistical analysis and data interpretation in your Excel projects.

Step-by-Step Guide: How to Find the Z-Score in Excel

Before calculating z-scores, you need to set up your Excel worksheet properly.

Setting up your data

1. Open a new Excel worksheet.
2. Enter your raw data in column A, starting from cell A2.
3. Label cell A1 as “Raw Data” to identify the column.

Calculating mean and standard deviation

To calculate z-scores, you need to know the mean and standard deviation of your dataset.

1. In cell B1, enter “Mean”.

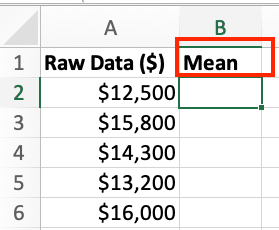
1. In cell B2, use the AVERAGE function to calculate the mean:
   Copy
   =AVERAGE(A2:A100)
    (Adjust the range to match your data)

1. In cell C1, enter “Standard Deviation”.

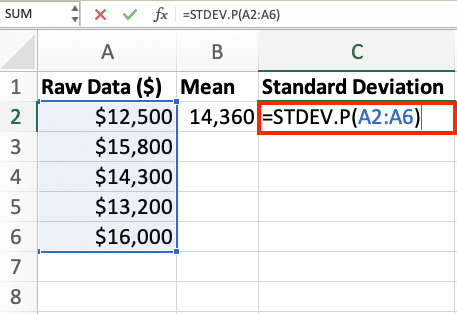
1. In cell C2, use the STDEV.P function to calculate the population standard deviation:
   Copy
   =STDEV.P(A2:A100)
    (Use STDEV.S for sample standard deviation if appropriate)

Creating columns for z-score calculation

1. In cell D1, enter “Z-Score”.

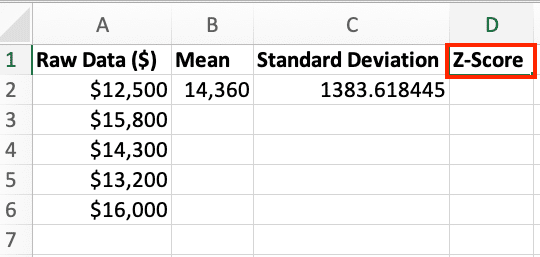
1. You’ll use column D to calculate the z-scores for each data point.

Step-by-Step Guide: Calculating Z-Scores in Excel

Using the basic z-score formula

To calculate z-scores manually using the formula:

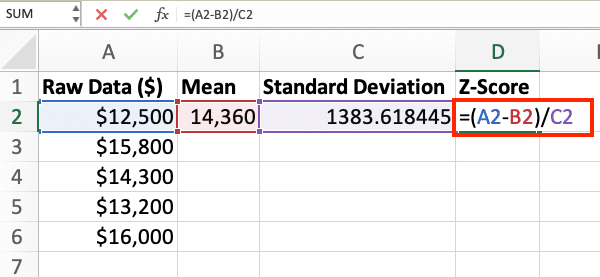
1. In cell D2, enter the following formula:
   Copy
   =(A2-$B$2)/$C$2

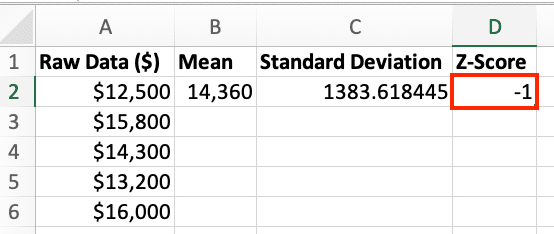
1. Press Enter. This calculates the z-score for the first data point.

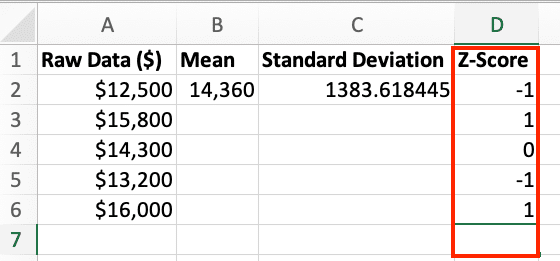
1. Edit the formula above for each column of the raw data to calculate the z-score

Implementing the STANDARDIZE function

Excel provides a built-in function for calculating z-scores:

1. In cell E1, enter “Z-Score (STANDARDIZE)”.
2. In cell E2, use the STANDARDIZE function:
   Copy
   =STANDARDIZE(A2,$B$2,$C$2)

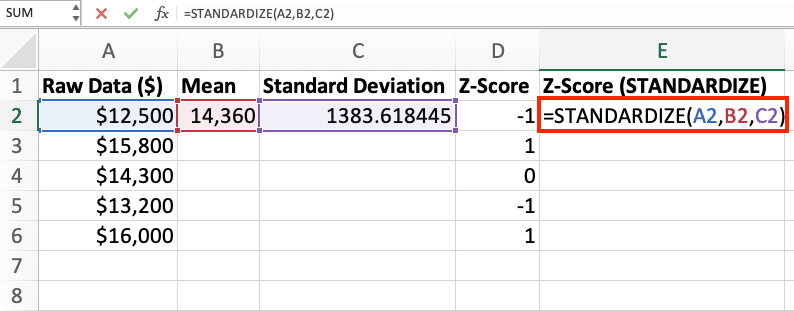
1. Edit the formula above for each column of the raw data to calculate the z-score

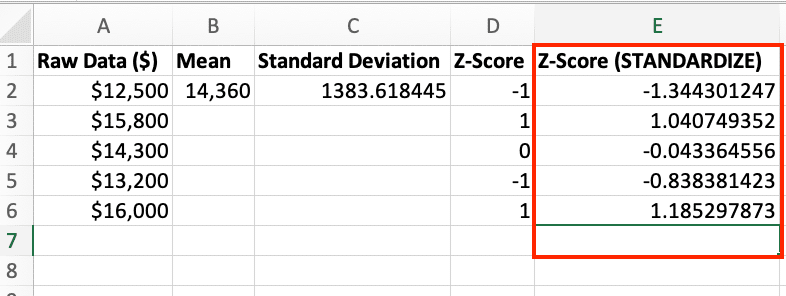
The STANDARDIZE function automatically calculates z-scores using the same formula we used manually.

Utilizing the Z.TEST function for probability

The Z.TEST function calculates the probability that a value from the dataset is greater than a specified z-score:

1. In cell F1, enter “Probability (Z.TEST)”.

1. In cell F2, use the Z.TEST function:
   Copy
   =Z.TEST(A2:A100,A2,$C$2)

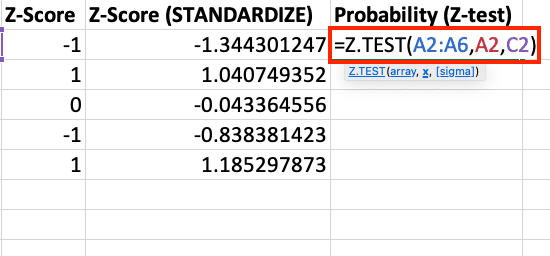
1. Edit the formula above for each column of the raw data to calculate the z-score

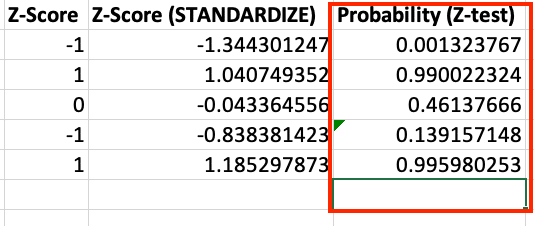
This calculates the probability of observing a value greater than each data point in your dataset.

Advanced Z-Score Techniques in Excel

Creating a z-score table

A z-score table shows the probability of a z-score occurring in a standard normal distribution:

1. In a new worksheet, create a column of z-scores from -4 to 4 in increments of 0.1.

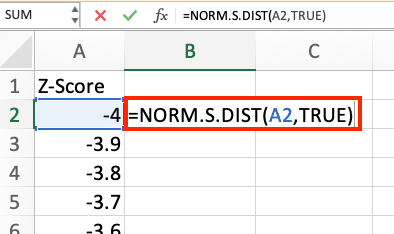
1. In the adjacent column, use the NORM.S.DIST function to calculate the cumulative probability:
   Copy
   =NORM.S.DIST(A2,TRUE)

1. Apply this formula to the entire column.

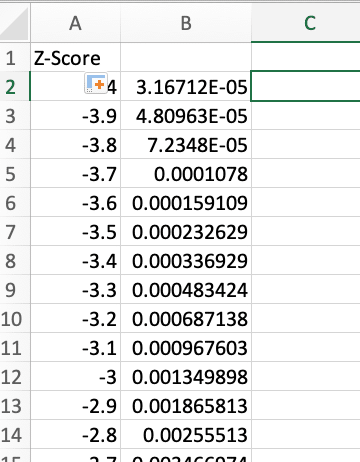
This table allows you to look up probabilities for specific z-scores quickly.

Converting z-scores to percentiles

To convert z-scores to percentiles:

1. In a new column, enter the formula:
   Copy
   =NORM.S.DIST(D2,TRUE)

1. Apply this formula to all z-scores in your dataset.

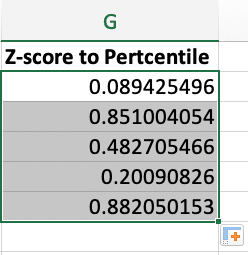
The result represents the percentage of values that fall below each data point in a standard normal distribution.

Calculating inverse z-scores

To find the raw score associated with a given z-score:

1. In a new column, use the NORM.INV function:
   Copy
   =NORM.INV(F2,$B$2,$C$2)

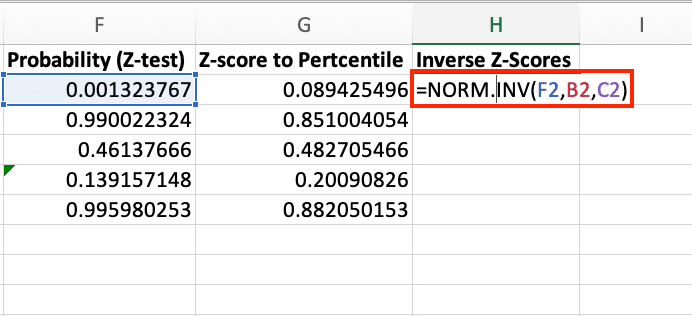
1. This formula calculates the raw score that corresponds to the probability calculated by Z.TEST.

Understanding Z-Scores: The Basics

What is a z-score?

A z-score, also known as a standard score, is a statistical measure that quantifies how many standard deviations an individual data point is from the mean of a dataset. It allows you to compare values from different datasets or distributions by standardizing them to a common scale.

Why are z-scores important?

Z-scores are crucial in statistical analysis for several reasons:

1. Standardization: They convert values from any normal distribution into a standard normal distribution, making it easier to compare data from different sources.
2. Outlier detection: Z-scores help identify unusual or extreme values in a dataset.
3. Probability calculation: They allow you to determine the likelihood of a particular value occurring in a dataset.
4. Performance comparison: Z-scores enable you to compare relative standings across different datasets.

The z-score formula explained

The formula for calculating a z-score is:

Copy

z = (x – μ) / σ

Where:

• z is the z-score
• x is the individual data point
• μ (mu) is the mean of the population
• σ (sigma) is the standard deviation of the population

This formula essentially measures how far a data point is from the mean in terms of standard deviations.

Beyond Z-Scores: Connecting Excel to Live Data

Excel provides tools for statistical analyses like z-scores, but businesses often need to work with data from multiple systems. Coefficient connects over 50 business systems directly to your spreadsheets. This allows you to sync live data, create real-time reports, and automate data updates in Excel. To see how this can improve your data analysis, check out Coefficient.